Théorie sur les Réseaux.
Avant d'aborder les Réseaux, nous allons voir certains points essentiels sans lesquels, il est impossible de comprendre ce qui se passe et quelles sont les raisons qui poussent à tant d'ingéniosité.
Les transmissions.
Dans une ligne de transmission, on est confronté à certains problèmes que l'on peut définir selon 5 points.
La vitesse de propagation.
La propagation est un des phénomènes les plus communs et des plus simples à comprendre. Lorsque l'on transmet un signal, quelque soit le type d'information (son, lumière, onde électromagnétique), il met impérativement un certain temps à se propager dans le milieu environnant, puisqu'il lui est impossible de se propager plus rapidement que la lumière et sa vitesse est freinée par le milieu traversé.
Par exemple, tout le monde connaît la vitesse de propagation du son dans l'air, puisqu'elle est de 1224 km/h (Mach 1). Mais peu de monde sait qu'elle est très différente dans l'eau puisqu'elle est alors de 5130 km/h (environ Mach 4). Comme quoi la vitesse de propagation d'une onde est liée au milieu traversé !
Ce phénomène, connu sous le nom de propagation dans les milieux isotropes, permet de définir quels seront les problèmes liés à la propagation d'une onde électromagnétique.
Il existe une théorie, établie par MAXWELL, qui en défini clairement les règles. Je ne vais pas présenter ici les équations (assez compliquées) de ce génie, je vais me contenter de vous présenter ce qui se passe intuitivement.
Dans un câble électrique, on définit 2 vitesses de propagation suivant le type d'information transmit. On trouve, d'une part, la vitesse de phase (Vj) qui représente la vitesse de propagation d'une onde monochromatique (une seule fréquence) et d'autre part, la vitesse de groupe (Vg) qui définit la variation de vitesse d'un paquet d'ondes en fonction de la fréquence de ses harmoniques (voir Fourrier).
Ces vitesses permettent de définir d'une part la forme des d'ondes à l'arrivée du signal, d'autre part, le temps mis par une onde pour se propager le long de la ligne.
En effet, la différence des vitesses pour différentes fréquences fait qu'un signal carré au départ est comme filtré à l'arrivée. Cela peut se traduire par un "circuit passe-bas" équivalent.
Fig. 3.
On résout généralement les problèmes de déformations liés aux vitesses de propagation en réalisant une mise en forme (détecteur à hystérésis) à la réception. Toutefois, cela entraîne un décalage temporel du signal.
Les atténuations dans les lignes.
Dans un câble électrique, on est confronté à un phénomène d'atténuation de l'amplitude des signaux, d’une part par effet Joules, mais aussi par filtrage. L’effet Joules est lié à la résistivité de la ligne, le filtrage aux effets inductifs et capacitifs de la ligne de transmission.
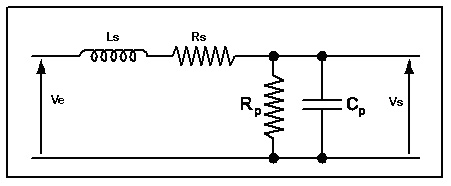
Ces éléments qui caractérisent les lignes sont liés, eux aussi, aux équations de MAXWELL (encore lui). Par l’utilisation de son modèle, on arrive à représenter une ligne de transmission par un schéma simple, le modèle du télégraphe (ce modèle tenant compte du phénomène de déphasage et du phénomène d'atténuation) :
Fig. 4. Modèle du télégraphe.
On y retrouve la structure d’un filtre passe bas. Où Rs est faible, Rp grande et où Ls et Cp sont liés aux matériaux utilisés et aux dimensions physiques de la ligne. Pour pouvoir en déduire la limite de longueur d’une ligne, il faut donc d’une part tenir compte de ce modèle, mais aussi de la capacité technologique a isoler un signal noyé dans le bruit.
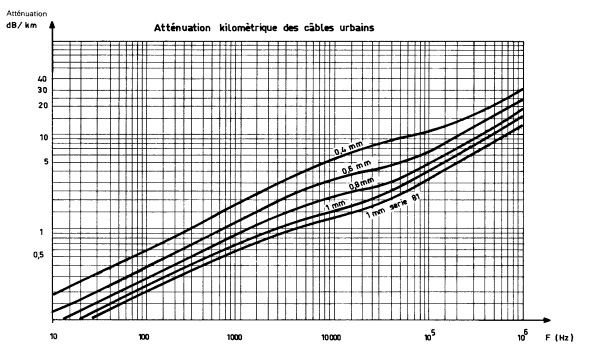
Fig. 5.
Exemple
d'atténuation dans un câble téléphonique Bande passante d'un canal.
Dans une ligne, on définit un élément très important qui va imposer bien des choix, ce paramètre est la bande passante. Elle définit la largeur du spectre que l'on peut faire transiter dans un canal sans que l'atténuation n'atteigne un niveau limite. On dispose selon les types de liaison de valeur allant de quelques Kbit/s à quelques Gbit/s.
Il convient aussi de considérer la bande de fréquence de transmission, c'est à dire les fréquences qui peuvent occuper un canal. Ainsi, si on analyse les différentes lignes, on peut définir pour chacune la gamme de fréquence transmise (par exemple pour la fibre optique où seules les ondes lumineuses de 400nm à 800nm sont transmissibles (ce qui correspond à des fréquences de 4 à 8 1014 Hz), une ligne bifilaire simple peut transmettre de 0 à 100MHz). Sur certaines autres lignes, c'est la structure technologique de l’émetteur ou du récepteur qui limite le domaine d'utilisation (l'utilisation d’un transformateur interdit la transmission des tensions continues et donc par conséquent la valeur moyenne du signal).
Pour d'autres raisons, on cherchera aussi à réduire au maximum la largeur du spectre de transmission, par exemple pour augmenter le nombre de dialogues simultanés sur une même ligne (voir multiplexage), mais aussi pour éviter de se trouver sur des fréquences spécifiques où le brouillage est fortement présent (par exemple 50Hz). Les réflexions dans les lignes.
C'est l'élément le plus préoccupant dans les transmissions puisque, si l'analyse des phénomènes d'atténuation et de déphasage montre qu'il suffit d'utiliser des éléments de mise en forme pour corriger ces déformations, les réflexions dans les lignes, nous confrontent à des problèmes autrement plus sérieux.
Ce phénomène est lié au rapport entre la longueur de la ligne de transmission et la longueur d'onde du signal transmis. C'est une transposition d'effets que l'on visualise en HF. Il convient donc de les comprendre par une approche simple de leur principe.
Les lignes ont une impédance
caractéristique définie par leur modèle équivalent. Ce n'est pas la résistance
linéique qui influence le plus, mais plutôt les composants réactifs (capacité et
inductance). En effet, la formule de cette impédance est la suivante :
Lorsqu'une onde atteint l'extrémité d'une ligne non terminée par un élément de résistance égale à l’impédance caractéristique, cette onde est réfléchie et reprend le chemin qu'elle a déjà parcouru. De retour à l'origine, elle peut à nouveau rebondir si cette extrémité aussi n'est pas adaptée, on a alors dans la ligne une onde qui va aller et venir, en rebondissant sur les extrémités de la ligne.
On définit 2 paramètres simple pour juger de la réflexion :
Le coefficient de réflexion :
Le coefficient de transmission : Ou ZC représente l’impédance de la charge et Z0 l’impédance caractéristique de la ligne.
Dans le cas d’une charge d’impédance 0Ω (court-circuit), on obtient :
Dans le cas d’une charge d’impédance infinie (circuit ouvert), on obtient :
Enfin dans le cas où la charge a la même valeur que l’impédance caractéristique, on obtient :
Exemples.
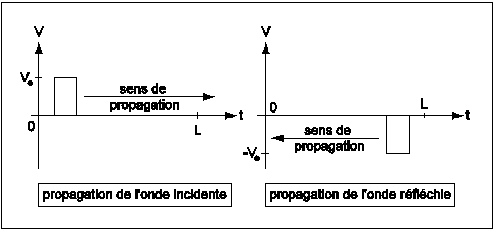
Cas d'une extrémité en court-circuit.
Dans le cas d'un court-circuit, l'onde se réfléchie en s'inversant
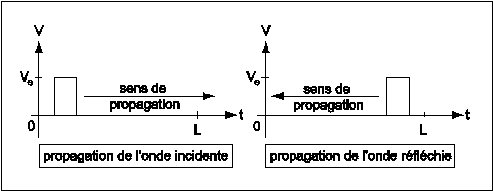
Cas d'une extrémité en l'air.
Dans le cas d'une extrémité en l'air, l'onde se réfléchie sans s'inverser.
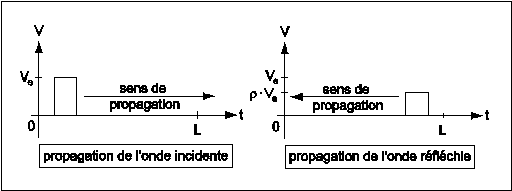
Cas d'une désadaptation par une impédance supérieure à l'impédance caractéristique
Dans ce cas, l'onde revient avec une amplitude plus faible, mais de même signe.
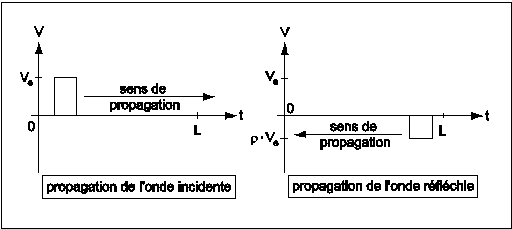
Cas d'une désadaptation par une impédance inférieure à l'impédance caractéristique
Dans ce cas, l'onde revient avec une amplitude plus faible, mais de signe opposé.
Cas d'adaptation.
Dans le cas d'une adaptation, il n'y a pas de réflexion.
Comme vous le constatez, sur une ligne, les effets des désadaptations sont parfois catastrophiques, non pas qu'ils soient destructifs mais à cause de leurs résultats sur la lisibilité des messages lors d'une superposition des ondes incidentes et réfléchies.
Cas de superposition d'ondes.
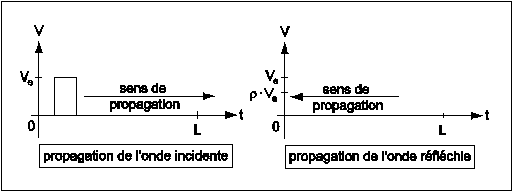
Rappel sur les réflexions dans les lignes.
On définit le coefficient de réflexion d'une extrémité de ligne par la formule suivante :
On définit aussi le coefficient de transmission (c'est à dire la part de l'onde incidente qui est transmise à l'obstacle) par la formule :
Où Zc est l'impédance vue à l'extrémité de la ligne, Z0 est l'impédance caractéristique, VR est l'onde réfléchie, VT l'onde transmise et VI l'onde incidente. Cette méthode n'est utilisable que pour des impédances purement résistives. Si on est confronté à des impédances réactives, l'utilisation d'une telle formule ne permet pas de se représenter le "chronogramme" ou la forme de l'onde circulant sur la ligne. On utilise alors la méthode de BERGERON.
Méthode du tableau.
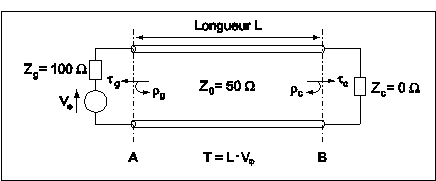
Soit le montage suivant :
rc est le coefficient de réflexion en B tandis que rg est le coefficient de réflexion en A. T est le temps que met l'onde pour se propager le long de la ligne. Dans notre exemple, on a : rc= -1 et rg= 1/3.
Par la méthode du tableau, on peut présenter l'évolution des ondes de la façon suivante :
Lorsqu'on connaît l'onde incidente, V1, on connaît alors l'amplitude de tous les signaux. Le bruit dans les lignes. Le bruit est un élément que nous
connaissons tous, il est le fruit de notre environnement
Pour lutter contre le bruit, il y a diverses méthodes, j'en citerai 4.
· Le blindage des lignes, c'est à dire leur protection contre les atteintes extérieures (solution utilisée en dernier recours, car problème de coût). · Une autre solution consiste à améliorer l'immunité au bruit en augmentant la puissance nécessaire à la détection des états logiques, par exemple en passant les signaux en ±12V (c'est la méthode la plus utilisée). · Une solution très industrielle, qui est très souvent utilisée dans les Réseaux locaux, consiste à ne plus coder les informations sous forme de tensions mais sous forme de courants (en utilisant des boucles de courant). En effet, la tension liée au bruit peut être très forte, mais le courant lui est généralement très faible · La dernière solution consistant à transmettre sur deux fils le signal de façon flottante. A l'arrivée, il suffit de mesurer la différence des tensions sur les 2 voies pour récupérer le signal d'origine en éliminant le bruit (qui est sensé être le même sur les 2 lignes, comme expliqué dans le chapitre suivant).
Il existe aussi d'autres bruits d'origine radiative (par exemple le 50Hz). Ils dépendent exclusivement de l'environnement local. |
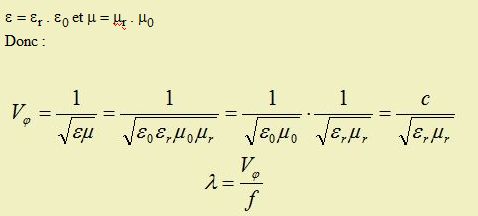

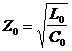

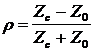

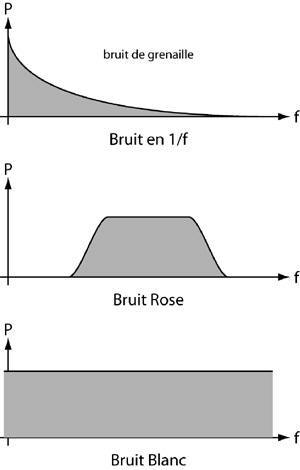 (lampes à décharges,
moteurs électriques, téléphonie et ondes hertzienne classiques, composants
électroniques, température,...) et couvre toute la gamme des fréquences
accessibles. Bien qu'en général, il soit considéré comme négligeable, il arrive
que certains bruits soient très forts (bruit à 50Hz) et puissent, du fait de
leur puissance, venir parasiter les installations électriques en général et les
Réseaux en particulier.
(lampes à décharges,
moteurs électriques, téléphonie et ondes hertzienne classiques, composants
électroniques, température,...) et couvre toute la gamme des fréquences
accessibles. Bien qu'en général, il soit considéré comme négligeable, il arrive
que certains bruits soient très forts (bruit à 50Hz) et puissent, du fait de
leur puissance, venir parasiter les installations électriques en général et les
Réseaux en particulier.