Les techniques de transmission de l'information.Dans ce chapitre, nous allons étudier toujours de le cadre de la transmission des données, comment on prépare ces données en vue d’une transmission où l'on peut grâce à un codage approprié améliorer la qualité, la vitesse ou la quantité des données transmises.
Le codage des informations.
Le codage des informations est utilisé dans les transmissions, aussi bien en bande de base qu'en bande décalée, pour éviter la transmission d'erreurs.
Une erreur étant toujours inacceptable, il convient pour l’éviter, de fournir, en plus des données, un code qui permet, dans le pire des cas, de détecter les erreurs et dans le meilleur, de les corriger.
Le codage de la parité.
Le code le plus simple pour transférer une information est le codage de la parité. Cette méthode, la plus élémentaire, fut l'une des premières à être utilisée.
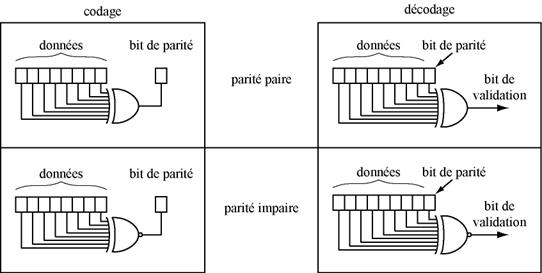
Son principe est assez simple, il s'agit d'ajouter un bit supplémentaire aux données transmises. Dans le cas d'une parité paire, ce bit permet au message d'être composé d'un nombre toujours pair de bits à '1', et dans le cas d'une parité impaire, un nombre toujours impaire de bits à '1'. Ce codage est réalisé au moyen de la fonction OU EXCLUSIF pour la parité paire et NON OU EXCLUSIF pour la parité impaire.
Au décodage, on va utiliser la même fonction logique que celle utilisée pour le codage pour valider le message. Par exemple avec la parité paire, on va réaliser une fonction OU EXCLUSIF entre les n bits du message et le bit de parité. Si le résultat vaut '0', le message est réputé vrai, si le résultat vaut '1' il est réputé faux.
Il faut toutefois relativiser ce résultat, en effet un code de parité ne sait détecter qu'un nombre impair d'erreur. Il lui est impossible de détecter deux erreurs. On considère donc que les codes de parité simple ne savent détecter qu'une seule erreur.
On peut aussi s'intéresser à la quantité de bits de contrôle transmis par message. Dans le cas d'un code de parité simple, on considère en général qu'il est dangereux de dépasser une proportion de 1/8 soit un bit de contrôle pour huit bits de données.
Une évolution des codes de parité consiste à introduire une redondance des codages.
Ainsi, on peut envisager, toujours en utilisant un contrôle de parité, de retrouver le bit erroné. Envisageons d'envoyer un message de 5 mots de 5 bits, on peut alors coder de la façon suivante le message.
Coté émission, à l'extrémité de chaque ligne, on place un bit de parité paire et on fait la même chose avec les colonnes.
On nomme parité transverse les bits de parités créés pour chaque colonne et parité longitudinale ceux créés pour chaque ligne.
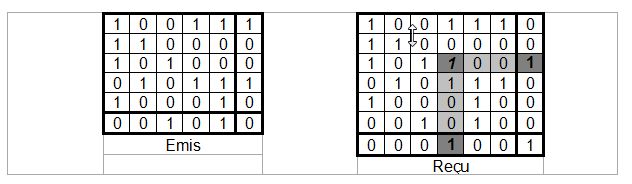
Les signaux émis sont : 100111 110000 101000 010111 100010 001010 Les signaux reçus sont : 100111 110000 101100 010111 100010 001010
A la réception, on récupère le message qui a été transmis et on lui applique encore une fois un contrôle de parité longitudinal et transverse. Si une erreur s'est glissée dans le code, immanquablement une parité longitudinale et une parité transverse sont à '1'. Cela signifie qu'il y a eut une erreur dans la transmission.
Dans notre exemple, en vérifiant les valeurs de contrôle, on constate qu'il y a 2 codes de contrôle non valable, l'un sur une ligne, l'autre sur une colonne. Donc on connaît rigoureusement l'emplacement de l'erreur.
Ce code permet donc de corriger l’erreur puisqu’elle est placée à l’intersection des 2 lignes et colonnes fautives. Toutefois, si à la réception, il y a deux ou trois erreurs, il y aura toujours systématiquement au moins un bit de parité transverse ou longitudinale à '1'. On peut donc détecter jusqu'à trois erreurs. Par contre, on ne peut corriger qu'une seule erreur.
La proportion des bits de contrôle par rapport aux bits de données, au moment de la transmission, passe (dans notre exemple) de 1/5 (0,2) pour une parité simple à 11/25 (0,44) pour les parités composées. Les codages redondants.
Les codages redondants augmentent le nombre de bits du message pour permettre de détecter d'éventuelles erreurs et éventuellement de les corriger.
Le code le plus connu est celui de HAMMING, bien que pratiquement abandonné, il fut le codes des premières transmissions numériques.
Exemple.
Imaginons que l'on cherche à transmettre un mot de 4 bits. Le code de HAMMING nous dit que pour n bits d'information, il faut k bits de contrôle pour corriger une erreur. On peut exprimer k en fonction de n grâce à la formule suivante :
Par itération, on peut résoudre cette équation. Pour n = 4, on a k = 3. Cela veut dire que l'on va transmettre 7 bits (m = k + n). Il faut maintenant coder les k bits en vue de la transmission.
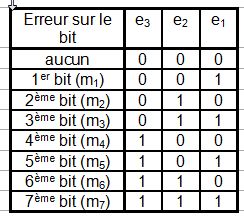
Pour cela on va coder dans un tableau toutes les possibilités d'erreur dans le message. Il y a pour un message de m bits, m+1 possibilité d'erreur. Ce tableau est composé de k (=3) colonnes. D'où la formule précédente (m+1 = n+k+1 et 2k représente le nombre de ligne identifiable avec k colonnes).
On sort maintenant les équations de e1, e2 et e3, et on trouve :
e1=m1 Å m3 Å m5 Å m7 e2=m2 Å m3 Å m6 Å m7 e3=m4 Å m5 Å m6 Å m7 Le signe Å signifie une addition modulo 2 ce qui peut se traduire par 1Å1=0. Å est l’opérateur Ou Exclusif Si l’on regarde bien, on se rend compte que les termes m1, m2 et m4 n’apparaissent qu’une seule fois dans les équations. On peut donc en faire (pour simplifier les équations) les trois bits de codage de Hamming.
Le message transmis étant alors composé de la façon suivante :
Pour terminer la réalisation de notre codage, il reste à remplir le tableau, c’est à dire trouver les valeurs de k1, k2 et k3 qui rendent e1, e2 et e3 nuls. En effet, le message n’étant pas encore émis, il n’est pas sensé contenir d’erreur.
Ce qui donne le tableau suivant :
A la réception, il suffit de calculer les valeurs de e1, e2 et e3 pour définir s’il y a eut une erreur et où elle se situe. On est alors capable de transmettre un message en détectant les erreurs et en les corrigeant.
Ainsi, si le message à envoyer est 1100, on a k3=0, k2=0 et k1=1 donc le message transmis est 1100001. Mais si en route, une erreur apparaît sur le 3ème bit, le message reçu devient 1100101, en utilisant le décodeur de Hamming, on trouve :
On sait donc où l’erreur se situe car e1, e2 et e3 indiquent une erreur sur le 3ème bit. On peut donc corriger le code reçu et écrire que le code sans erreur est 1100001 donc que le message est 1100.
Avec ce code de Hamming, on sait donc corriger une erreur sur un bit mais on est capable, sans les corriger, de détecter jusqu'à trois erreurs.
Quand à la proportion des bits de contrôle, on constate que plus n est grand, plus k augmente, mais pas de façon linéaire. Par exemple, si pour détecter 3 erreurs, il y a besoin de 3 bits de contrôle pour 4 bits de données, avec 112 bits de données, il suffit d'utiliser 7 bits de contrôle.
Attention, rappelons que la probabilité d'erreur s'accroît linéairement avec le nombre de bits transmis. Pour une transmission de 119 bits, le risque d'erreur est donc 17 fois plus grand que pour une transmission de 7 bits. Aussi, pour une telle quantité de données, il serait raisonnable d'utiliser un code de Hamming plus puissant, c'est à dire capable de détecter plus d'erreur. Les codes CRC.
Les codes CRC ou CYCLICAL REDUNDANCY CHECK (contrôle par redondance cyclique) sont basés sur une série d'opérations arithmétiques.
Tout commence par l'élaboration de
la forme polynomiale du message binaire. Par exemple, 110100, c'est à dire
s'écrit sous forme polynomiale x5+x4+x2. On nomme ce polynôme P(x). Puis on applique la formule suivante :
Où G(x) est un polynôme, défini par le protocole du Réseau, connu de l'émetteur et du récepteur et de degré v. Q(x) est le quotient de la division de P(x).xv par G(x) et donc R(x) est le reste de la division. Puisque G(x) est de degré v, R(x) est forcément d'un degré inférieur ou égal à v. C'est ce reste R(x) qui va être transmis en plus de P(x) au récepteur.
A l'arrivée, on connaît donc R(x) (le reste transmis avec le message), v (qui est obtenu par analyse de G(x)), G(x) (connu par définition) et P(x) (le message transmis). On va alors refaire le même calcul que celui réalisé par l'émetteur et comparer les restes des deux divisions.
S’il y a une différence entre les deux restes, on est sûr alors qu'une erreur s'est glissée dans la transmission.
G(x) est défini par la norme de transmission utilisée. L'avis V41 de la norme CCITT (Comité Consultatif International pour le Télégraphe et le Téléphone) définit G(x) comme : G(x)=x16+x12+x5+1
Pour le Réseau CAN, le code G(x) vaut x15+x14+x10+x8+x7+x4+x3+1
Et c'est là que l'on constate l'efficacité du code CRC, puisque dans le cas du bus CAN, il permet de repérer les erreurs suivantes :
· Toutes les salves d'erreurs comportant un nombre impair de termes · Toutes les salves d'erreurs comportant moins de 17 bits. · 99,998% des salves d'erreurs de plus de 16 bits.
C'est ce qui fait que le codage CRC est très utilisé pour les supports peu fiables, mais aussi dans la majeure partie des Réseaux.
Du point de vue des proportions entre le nombre de bits de données et le nombre de bits de contrôle, on constate que, par exemple, le Réseau Ethernet utilise un code CRC de 32 bits qui lui permet d'assurer la sécurité de sa trame de donnée qui peut contenir jusqu'à 1526 octets, soit un rapport de 4/1526 (0,0026).
Plus généralement, les codes CRC sur 64 bits sont utilisés par les logiciels de compression de données (ZIP ou RAR) pour valider des fichiers pouvant atteindre plusieurs dizaine de Méga octets.
Correction d'erreurs de transmission.
Dans le monde des Réseaux, les codes ne sont là que pour détecter les erreurs de transmission, même si ils sont capables de les corriger. La capacité de transfert des Réseaux moderne, et la sensibilité des données, sont telles que l'on préfère retransmettre un paquet si il est susceptible de contenir des erreurs plutôt que d'en commettre de nouvelles par des corrections hasardeuses.
|